偏差値について

トップ
ブログ
偏差値について

偏差値について

2020/03/01

前回まで、東京の私立中学校のお話してきましたが、今回は「偏差値」についてお話しようと思います。
「偏差値」と言えば、中学や高校受験のときに受験する学校のレベルを判断するのに使う指標として使われることが多いかも思います。

そもそも、偏差値とは何なのでしょうか？

、

まず、テストの評価基準としてよく使われるのは「平均点」です。
この「平均点」より上か下かを一つの判断基準にされることが多いかと思います。
ただ、実際にはテストによって点数のばらつきがあり、このばらつきを考慮して点数の価値を
位置付けたものが「偏差値」ということになります。
また、このばらつきのことを「標準偏差」と言います。
「標準偏差」が小さければ、点数差が少なく平均点近くに点数が偏っており、大きい場合は
点数にばらつきがあるということになります。

なお、「標準偏差」とは、細かい統計的なお話しは省きますが、平均点との各受験者の点数の差を
総合的に表したものと考えていただいて結構です。

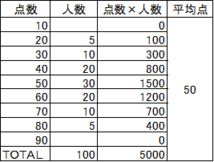
例えば、１００人の受験生がいて、２種類のテストを受験し、平均点は同じ５０点だったとします。
ただし、「テスト１」はばらつきが大きく標準偏差は１４．５、「テスト２」は標準偏差は９．５でした。　
　テスト１　　　　　　　　　　　
　

　
　
　テスト２
　

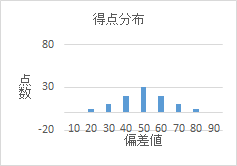
この場合、例えば、点数が７０点だった人は「テスト１」だと偏差値が６４、「テスト２」だと偏差値は７１となり、同じ平均点で同じ点数であってもその価値が違ってきます。

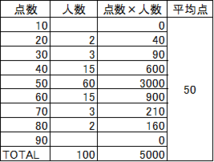
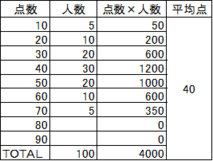
もう１例として、「標準偏差」は同じ（１７．６）で「平均点」が違った場合のお話をしておきます。
「テスト３」と「テスト４」はばらつきは同じ（「標準偏差」が同じ）ですが、平均点が「テスト３」は４０点、「テスト４」は６０点で平均点が２０点も違うようなテストだっということになります。

　テスト３
　

　テスト４
　

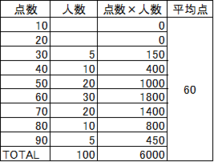
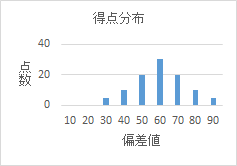
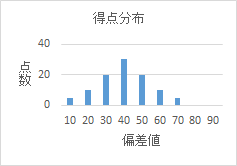
この場合、同じ受験者層であったとすると、「テスト３」はちょっと難しく平均点が低めで「テスト４」は易しめの問題で平均点が高かったということになります。
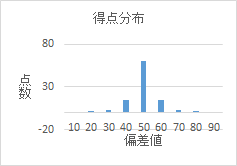
この場合、それぞれのテストで７０点をとったとすると偏差値は「テスト３」では６７、「テスト４」では５６となり、７０点の価値はそれぞれのテストで変わってきます。

最後に偏差値により全体のどのくらいに位置しているのかというお話をいたします。
十分な母数（テストの場合は受験者数ですね・・）があって特異なばらつきのないテストの場合
統計的には一般的に「正規分布」という形の分布に近くなると考えられています。
この分布では平均±「標準偏差」に全体の６８％、平均±２×「標準偏差」に９５％、平均±３×「標準偏差」に９９．７％とほとんどの受験生が含まれることになります。

　

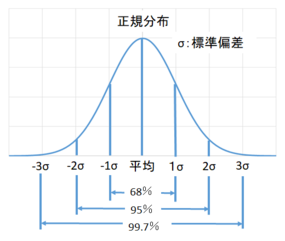
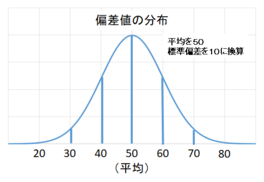
これを偏差値で置き換えると平均は５０ですから偏差値２０～８０の間に９９．７％の生徒が含まれることになります。
偏差値７０以上は上位２．５％ほど（５％の半分）となり、偏差値８０以上となると上位０．１５％となりあます。テストが満点の場合、テストの難易度によって偏差値が変わってきます。
（テストが易しければ偏差値は低めに、難しければ高めの偏差値になります。）、

　

「偏差値」はこのようにあるテストでの点数のばらつきを考慮した相対的な評価値ではありますが、そもそも点数や偏差値だけで理解度を確認するのではなく、どういう問題でどこを間違ったのかを確認することが重要だと思います。
また、「偏差値」は相対的な指数ですので、受験層のレベルが高い場合、偏差値は低くなります。
中学受験用の模試(首都圏模試、日能研模試、四谷大塚模試等）では相対的にレベルが高いですし、各模擬テストにより偏差値が１０くらい違ったりします。
絶対的な指標ではありませんので、ご注意ください。

ご参考まで。

中学・高校受験対策　個別学習塾
セルモ羽根木教室
　

ブログ一覧